Question

The following chart represents the record low temperatures recorded in Phoenix for April-November. Select the answer below that best describes the mean and the median of the data set (round answers to the nearest tenth). A graph titled Phoenix Low Temperatures has month on the x-axis and temperature (degrees Fahrenheit) on the y-axis. April, 32; May, 40; June, 50; July, 61; August, 60; September, 47; October, 34; November, 25. a. The mean is 43.5°F, and the median is 43.6°F. b. The mean is 60.5°F, and the median is 60.5°F. c. The mean is 60°F, and the median is 61°F. d. The mean is 43.6°F, and the median is 43.5°F.

Answer 1

it is d

Explanation:

Answer 2

d. The mean is 43.6°F, and the median is 43.5°F.

Explanation:

Hello!

The data corresponds to the low temperatures in Phoenix recorded for April to November.

April: 32ºF

May: 40ºF

June: 50ºF

July: 61ºF

August: 60ºF

September: 47ºF

October: 34ºF

November: 25ºF

Sample size: n= 8 months

The mean or average temperature of the low temperatures in Phoenix can be calculated as:

`\frac{}{X}`= ∑X/n= (32+40+50+61+60+47+34+25)/8= 43.625ºF (≅ 43.6ºF)

The Median (Me) is the value that separates the data set in two halves, first you have to calculate its position:

PosMe= (n+1)/2= (8+1)/2= 4.5

The value that separates the sample in halves is between the 4th and the 5th observations, so first you have to order the data from least to greatest:

25; 32; 34; 40; 47; 50; 60; 61

The Median is between 40 and 47 ºF, so you have to calculate the average between these two values:

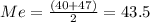`Me= ((40+47))/(2) = 43.5` ºF

The correct option is D.

I hope this helps!