Question

Find the value of x and the value of y

A. X=20,y=45
B. X=45,y=20
C. X=60,y=120
D. X=90,y=60

Answer 1

X=45 , y=20

Option B is the right option.

Solution,

Shown quadrilateral is a trapezoid.

2x and the right angle are consecutive interior angles because they are on the same side of a transversal and between likes that the transversal Intersects.

Since, 2x° and the right angles are consecutive interior angles and two of the lines form these angles are parallel, then by consecutive interior angles theorem the two angles are supplementary and thus the sum of their measure is 180°

`2x + 90 = 180`

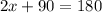
Subtracting 90 on both sides:

`2x + 90 - 90 = 180 - 90 \\ 2x = 90`

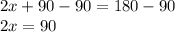
dividing both sides by 2

`(2x)/(2) = (90)/(2) \\ x = 45`

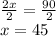
Also,

`3y + 6y = 180 \\ 9y = 180`

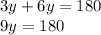
dividing both sides by 9

`(9y)/(9) = (180)/(9) \\ y = 20`

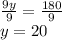
hence, The value of X and y are 45° and 20° respectively..

Hope this helps....

Good luck on your assignment....

Answer 2

B. x=45, y=20

Explanation:

Angles in a quadrilateral add up to 360 degrees.

One angle is a right angle = 90 degrees.

2x + 3y + 6y + 90 = 360

2x + 9y + 90 = 360

2x + 9y = 270

Plug x as 20 and y as 45.

2(20) + 9(45) = 270

445 = 270

Wrong.

Plug x as 45 and y as 20.

2(45) + 9(20) = 270

270 = 270

Correct.

Plug x as 60 and y as 120.

2(60) + 9(120) = 270

1200 = 270

Wrong.

Plug x as 90 and y as 60.

2(90) + 9(60) = 270

720 = 270

Wrong.