Answer:
k = -11
Explanation:
Let
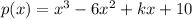
And x+2 is a factor of p(x)
Let x+2 = 0 => x = -2
Putting in p(x)
=> p(-2) =
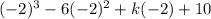
By remainder theorem, Remainder will be zero
=> 0 = -8-6(4)-2k+10
=> 0 = -8-24+10-2k
=> 0 = -22-2k
=> -2k = 22
Dividing both sides by -2
=> k = -11