Question

darius is camping in the woods. he notices on a map that his campsite is 50 yards from the ranger station. he walks 18 yards towards the ranger station the tree forms the altitude of a right triangle that connects the top of the tree darius's campsite, and the ranger station. sketch a diagram of the situation and determine the angle of depression formed by darius sightline to the ranger station.

Answer 1

The angle of depression formed by Darius's sight line to the ranger station is 53.13°.

Explanation:

Denote Darius's camp site as C, the ranger station as R and the tree as T.

Consider the triangle CTR.

TX is the altitude of the right angled triangle TXR.

The altitude of a right angled triangle forms two triangle that similar to each other.

So, ΔTXC
`\sim` ΔTXR.

Compute the measure of TX as follows:

`(CX)/(TX)=(TX)/(RX)\\\\TX^(2)=CX* RX\\\\TX=√(CX* RX)`

`=√(18* 32)\\\\=24\ \text{yd}`

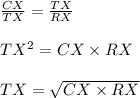
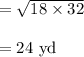
The angle d represents the angle of depression formed by Darius's sight line to the ranger station.

Compute the value of d as follows:

`tan\ d^(o)=(RX)/(TX)\\\\d^(o)=tan^(-1) [(RX)/(TX)]`

`=tan^(-1) [(32)/(24)]\\\\=53.13`

Thus, the angle of depression formed by Darius's sight line to the ranger station is 53.13°.