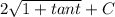Question

Help with one integral problem?

Answer 1

Answer:
`2√(1+tant)+C`

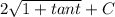
Explanation:

To integrate means to find the antiderivative of the function. For this problem, we can use u-substitution.

`\int\limits {(dt)/(cos^2t√(1+tant) ) } \`

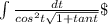
Let's first use our identities to rewrite the function. Since
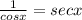`(1)/(cosx) =secx`, we can use this identity.

`\int\limits {(sec^2t)/(√(1+tant) ) } \,`

`u=√(1+tant)`

`du=(sec^2t)/(2√(1+tant) ) dt`

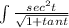
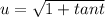
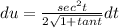
Now that we have u and du, we can plug them back in.

`\int\limits {2} \, du`

`\int\limits{2} \, du=2u`

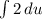
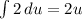
Since we know u, we can plug that in.

`2√(1+tant)`

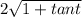
This may seem like the correct answer, but we forgot to add the constant.

`2√(1+tant)+C`