Question

PLEASE HELP ASAP Brent is driving to a conference in another state. Three hours after leaving his home and beginning his drive, Brent is still 470 miles from his destination. After another 4 hours of driving, Brent is 258 miles from his destination. After 9 hours of driving, Brent plans to stop at a hotel for the night and begin his trip again 12 hours later. If Brent’s average speed had been faster or slower on his trip, what features of the graph would change and how would they change in each situation. Explain your answers. Type your response here: Brent decided that he needed to reach his destination in 11 hours of driving. What would his average rate of speed, rounded to the nearest hundredth, need to be to accomplish this? Show your work.

Answer 1

WHAT DOES THE SLOPE OF THE LINE REPRESENT????

Explanation:

Answer 2

The average rate of speed needed is 76 miles/hr.

Explanation:

From the provided data, we can conclude two points:

• Brent is 470 miles from his destination after driving for 3 hours, (3, 470).

• Brent is 258 miles from his destination after driving for 7 hours, (7, 258).

Form an equation representing the distance left to Brent's destination, d, based on the amount of time he has spent driving, t.

`(d-d_(1))=(d_(2)-d_(1))/(t_(2)-t_(1))\cdot (t-t_(1))\\\\(d-470)=(258-470)/(7-3)\cdot (t-3)\\\\d-470=-53(t-3)\\\\d=-53t+159+470\\\\d=629-53t`

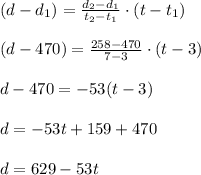
The speed of a vehicle is:

`speed=(distance)/(time)\\\\\Rightarrow distance=speed* time`

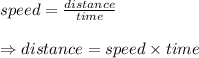
So distance is directly proportional to the speed, i.e. as speed increases the distance covered also increases and as speed decreases the distance covered also decreases.

So, if Brent’s average speed had been faster or slower on his trip, the distance left to be covered would decrease or increase accordingly.

Consider the provided information:

3 hours of driving → 470 miles left

7 hours of driving → 258 miles left.

That in 4 hours Brent covered 212 miles.

Speed at which he was driving was:

`speed=(distance)/(time)=(212)/(4)=53\ \text{miles/hr}`

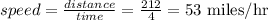
Now it is provided that after 9 hours of driving, Brent plans to stop at a hotel for the night.

That is he drove for another 2 hours at the same speed, i.e. 53 miles/hr.

Compute the distance covered between 7 hour to 9 hour as follows:

`distance = speed* time=53* 2=106\ \text{miles}`

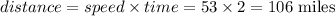
Remaining distance = 258 - 106 = 152 miles.

If Brent wants to reach his destination in 11 hours of driving then he has to cover the remaining 152 miles in the next 2 hours.

Compute the speed as follows:

`speed=(distance)/(time)=(152)/(2)=76\ \text{miles/hr}`

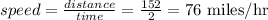
Thus, the average rate of speed needed is 76 miles/hr.