Answer:
The corresponding definite integral may be written as

The answer of the above definite integral is

Explanation:
The given limit interval is
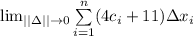
![[a, b] = [-8, 6]](https://img.qammunity.org/2021/formulas/mathematics/college/jjpy79lb7onuwr2n1l61si7ahgsoajtfok.png)
The corresponding definite integral may be written as


Bonus:
The definite integral may be solved as

Therefore, the answer to the integral is
