Question

Troy has two $1, two $2, and ten $3 gift certificates. If he selects three bills in succession, what is the probability that a $1 gift certificate is selected, then a $ 3 gift certificate and then a $2 gift certificate if replacement does not take place? and is the answer dependant or independant?

Answer 1

A. dependent 5/273

Explanation:

just got it right

Answer 2

`(5)/(273)`

They are dependent events.

Explanation:

Given:

Number of $1 gift certificates = 2

Number of $2 gift certificates = 2

Number of $3 gift certificates = 10

To find:

Probability that a $1 gift certificate is selected, then a $3 and then a $2 certificate is selected = ?

Solution:

First of all, let us learn about the formula of probability of any event E:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

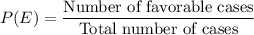
Finding probability of choosing $1 gift certificate in the first turn:

Number of favorable cases or number of $1 gift certificates = 2

Total number of cases or total number gift certificates = 2 + 2 + 10 = 14

So, required probability =
`(2)/(14) \Rightarrow (1)/(7)`

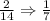
Finding probability of choosing $3 gift certificate in the 2nd turn:

Number of favorable cases or number of $1 gift certificates = 10

Now, one gift certificate is already chosen,

So, Total number of cases or total number gift certificates = 14 - 1 = 13

So, required probability =
`(10)/(13)`

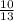
Finding probability of choosing $2 gift certificate in the 3rd turn:

Number of favorable cases or number of $2 gift certificates = 2

Now, two gift certificates is already chosen,

So, Total number of cases or total number gift certificates = 14 - 2 = 12

So, required probability =
`(2)/(12) \Rightarrow (1)/(6)`

Probability that a $1 gift certificate is selected, then a $3 and then a $2 certificate is selected:

`(1)/(7)* (10)/(13)* (1)/(6)\\\Rightarrow (5)/(273)`

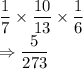
They are dependent events because total number of cases and total number of favorable cases depend on the previous chosen gift certificate.

So, the answer is:

`(5)/(273)`

They are dependent events.