Question

A certain radioactive isotope decays at a rate of 0.2​% annually. Determine the ​half-life of this​ isotope, to the nearest year.

Answer 1

The half-life of the radioactive isotope is 346 years.

Step-by-step explanation:

The decay rate of the isotope is modelled after the following first-order linear ordinary differential equation:

`(dm)/(dt) = -(m)/(\tau)`

Where:

`m` - Current isotope mass, measured in kilograms.

`t` - Time, measured in years.

`\tau` - Time constant, measured in years.

The solution of this differential equation is:

`m(t) = m_(o)\cdot e^{-(t)/(\tau) }`

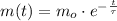
Where
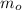`m_(o)` is the initial mass of the isotope. It is known that radioactive isotope decays at a yearly rate of 0.2 % annually, then, the following relationship is obtained:

`\%e = (m(t)-m(t+1))/(m(t))* 100\,\% = 0.2\,\%`

`1 - (m(t+1))/(m(t)) = 0.002`

`1 - \frac{m_(o)\cdot e^{-(t+1)/(\tau) }}{m_(o)\cdot e^{-(t)/(\tau) }}=0.002`

`1 - e^{-(1)/(\tau) } = 0.002`

`e^{-(1)/(\tau) } = 0.998`

`-(1)/(\tau) = \ln 0.998`

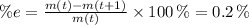
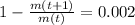
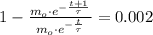
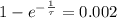
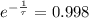
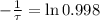
The time constant associated to the decay is:

`\tau = -(1)/(\ln 0.998)`

`\tau \approx 499.500\,years`

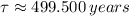
Finally, the half-life of the isotope as a function of time constant is given by the expression described below:

`t_(1/2) = \tau \cdot \ln 2`

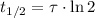
If
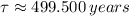`\tau \approx 499.500\,years`, the half-life of the isotope is:

`t_(1/2) = (499.500\,years)\cdot \ln 2`

`t_(1/2)\approx 346.227\,years`

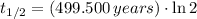
The half-life of the radioactive isotope is 346 years.