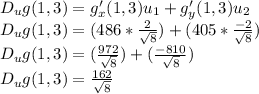Question

Find the directional derivative of at the point (1, 3) in the direction toward the point (3, 1). g

Answer 1

Complete Question:

Find the directional derivative of g(x,y) =
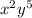`x^2y^5`at the point (1, 3) in the direction toward the point (3, 1)

Answer:

Directional derivative at point (1,3),
`D_ug(1,3) = (162)/(√(8) )`

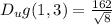
Explanation:

Get
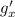`g'_x` and
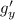`g'_y` at the point (1, 3)

g(x,y) =
`x^2y^5`

`g'_x = 2xy^5\\g'_x|(1,3)= 2*1*3^5\\g'_x|(1,3) = 486`

`g'_y = 5x^2y^4\\g'_y|(1,3)= 5*1^2* 3^4\\g'_y|(1,3)= 405`

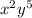
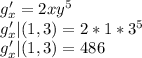
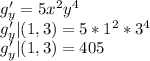
Let P = (1, 3) and Q = (3, 1)

Find the unit vector of PQ,

`u = \frac{\bar{PQ}}{|\bar{PQ}|} \\\bar{PQ} = (3-1, 1-3) = (2, -2)\\{|\bar{PQ}| = √(2^2 + (-2)^2)\\`

`|\bar{PQ}| = √(8)`

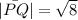
The unit vector is therefore:

`u = ((2, -2))/(√(8) ) \\u_1 = (2)/(√(8) ) \\u_2 = (-2)/(√(8) )`

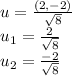
The directional derivative of g is given by the equation:

`D_ug(1,3) = g'_x(1,3)u_1 + g'_y(1,3)u_2\\D_ug(1,3) = (486*(2)/(√(8) ) ) + (405*(-2)/(√(8) ) )\\D_ug(1,3) = ((972)/(√(8) ) ) + ((-810)/(√(8) ) )\\D_ug(1,3) = (162)/(√(8) )`