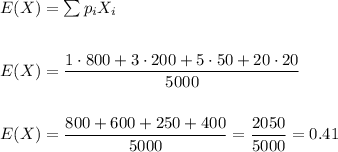Answer:
The expected value of this raffle if you buy 1 ticket is $0.41.
Explanation:
The expected value of the raffle if we buy one ticket is the sum of the prizes multiplied by each of its probabilities.
This can be written as:
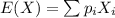
For example, the first prize is $800 and we have only 1 prize, that divided by the number of tickets gives us a probability of 1/5000.
If we do this with all the prizes, we can calculate the expected value of a ticket.