Question

Use the data below, showing a summary of highway gas mileage for several observations, to decide if the average highway gas mileage is the same for midsize cars, SUV’s, and pickup trucks. Test the appropriate hypotheses at the α = 0.01 level.

n Mean Std. Dev.
Midsize 31 25.8 2.56
SUV’s 31 22.68 3.67
Pickups 14 21.29 2.76

Answer 1

Explanation:

Hello!

You need to test at 1% if the average highway gas mileage is the same for three types of vehicles (midsize cars, SUV's and pickup trucks) to compare the average values of the three groups altogether, you have to apply an ANOVA.

n | Mean | Std. Dev.

Midsize | 31 | 25.8 | 2.56

SUV’s | 31 | 22.68 | 3.67

Pickups | 14 | 21.29 | 2.76

Be the study variables :

X₁: highway gas mileage of a midsize car

X₂: highway gas mileage of an SUV

X₃: highway gas mileage of a pickup truck.

Assuming these variables have a normal distribution and are independent.

The hypotheses are:

H₀: μ₁ = μ₂ = μ₃

H₁: At least one of the population means is different.

α: 0.01

The statistic for this test is:

`F= (MS_(Treatment))/(MS_(Error))`~
`F_(k-1;n-k)`

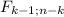
Attached you'll find an ANOVA table with all its components. As you see, to manually calculate the statistic you have to determine the Sum of Squares and the degrees of freedom for the treatments and the errors, next you calculate the means square for both and finally the test statistic.

For the treatments:

The degrees of freedom between treatments are k-1 (k represents the amount of treatments):
`Df_(Tr)= k - 1= 3 - 1 = 2`

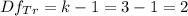
The sum of squares is:

SSTr: ∑ni(Ÿi - Ÿ..)²

Ÿi= sample mean of sample i ∀ i= 1,2,3

Ÿ..= grand mean, is the mean that results of all the groups together.

So the Sum of squares pf treatments SStr is the sum of the square of difference between the sample mean of each group and the grand mean.

To calculate the grand mean you can sum the means of each group and dive it by the number of groups:

Ÿ..= (Ÿ₁ + Ÿ₂ + Ÿ₃)/ 3 = (25.8+22.68+21.29)/3 = 23.256≅ 23.26

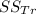`SS_(Tr)`= (Ÿ₁ - Ÿ..)² + (Ÿ₂ - Ÿ..)² + (Ÿ₃ - Ÿ..)²= (25.8-23.26)² + (22.68-23.26)² + (21.29-23.26)²= 10.6689

`MS_(Tr)= (SS_(Tr))/(Df_(Tr))= (10.6689)/(2)= 5.33`

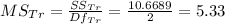
For the errors:

The degrees of freedom for the errors are:
`Df_(Errors)= N-k= (31+31+14)-3= 76-3= 73`

The Mean square are equal to the estimation of the variance of errors, you can calculate them using the following formula:

`MS_(Errors)= S^2_e= ((n_1-1)S^2_1+(n_2-1)S^2_2+(n_3-1)S^2_3)/(n_1+n_2+n_3-k)= ((30*2.56^2)+(30*3.67^2)+(13*2.76^2))/(31+31+14-3) = (695.3118)/(73)= 9.52`

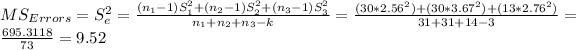
Now you can calculate the test statistic

`F_(H_0)= (MS_(Tr))/(MS_(Error)) = (5.33)/(9.52)= 0.559= 0.56`

The rejection region for this test is always one-tailed to the right, meaning that you'll reject the null hypothesis to big values of the statistic:

`F_(k-1;N-k;1-\alpha )= F_(2; 73; 0.99)= 4.07`

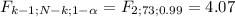
If
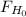`F_(H_0)` ≥ 4.07, reject the null hypothesis.

If
`F_(H_0)` < 4.07, do not reject the null hypothesis.

Since the calculated value is less than the critical value, the decision is to not reject the null hypothesis.

Then at a 1% significance level you can conclude that the average highway mileage is the same for the three types of vehicles (mid size, SUV and pickup trucks)

I hope this helps!