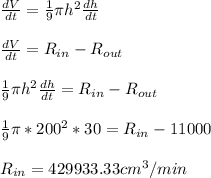Question

) Water is leaking out of an inverted conical tank at a rate of 11,000 cm3/min at the same time that water is being pumped into the tank at a constant rate. The tank has height 12 m and the diameter at the top is 8 m. If the water level is rising at a rate of 30 cm/min when the height of the water is 2 m, find the rate at which water is being pumped into the tank. Give your answer in units of cm and min and round to the nearest whole number. (Write your answer in a complete sentence).

Answer 1

Rate at which water is being pumped into the tank,
`R_(in) = 429933.33 cm^3/min`

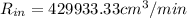
Step-by-step explanation:

Rate at which water is leaking out,
`R_(out) = 11, 0000 cm^3/min`

Height of the tank, h = 12 m

The top diameter of the tank, d = 8 m = 800 cm

The top radius of the tank, r = d/2 = 800/2 = 400 cm

The rate of change of water height, dh/dt = 30 cm/min

Height of water = 2 m

By carefully observing the diagram contained in the file attached to this solution, using the property of similar triangle:

h/r = 12/4

r = h/3

Since the tank is conical, volume of the water at time, t will be:

`V = (1)/(3) \pi r^(2) h\\\\V = (1)/(3) \pi ((h)/(3) )^(2) h\\\\V = (1)/(27) \pi h^(3) \\`

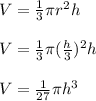
Finding the derivative of the above with respect to t to get the rate of change in the volume of water.

`(dV)/(dt) = (1)/(9) \pi h^(2) (dh)/(dt) \\\\(dV)/(dt) = R_(in) - R_(out) \\\\(1)/(9) \pi h^(2) (dh)/(dt) = R_(in) - R_(out)\\\\(1)/(9) \pi * 200^(2)* 30 = R_(in) - 11000\\\\ R_(in) = 429933.33 cm^3/min`