Question

For what values of k does the function y = cos(kt) satisfy the differential equation 81y'' = -100y? k = (smaller value) k = (larger value)

Answer 1

k = -10/9 and k = 10/9

Explanation:

given y = cos(kt) and the differential equation 81y'' = -100y

y' = -ksin(kt)

y'' = -k²cos(kt)

Substituting the value of y and y'' in the differential equation we have;

81 (-k²cos(kt))= -100 (cos(kt))

-81k²cos(kt)) = -100cos(kt))

-81k² = -100

k² = 100/81

k = ±
`\sqrt{(100)/(81) }`

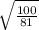
k = ±10/9

k = -10/9 and k = 10/9