Answer:
A 90% confidence interval for the standard deviation of the fracture toughness distribution is [4.06, 6.82].
Explanation:
We are given the following observations that were made on fracture toughness of a base plate of 18% nickel maraging steel below;
68.6, 71.9, 72.6, 73.1, 73.3, 73.5, 75.5, 75.7, 75.8, 76.1, 76.2, 76.2, 77.0, 77.9, 78.1, 79.6, 79.8, 79.9, 80.1, 82.2, 83.7, 93.4.
Firstly, the pivotal quantity for finding the confidence interval for the standard deviation is given by;
P.Q. =
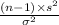 ~
~

where, s = sample standard deviation =
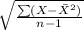 = 5.063
= 5.063
 = population standard deviation
= population standard deviation
n = sample of observations = 22
Here for constructing a 90% confidence interval we have used One-sample chi-square test statistics.
So, 90% confidence interval for the population standard deviation,
 is ;
is ;
P(11.59 <
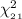 < 32.67) = 0.90 {As the critical value of chi at 21 degrees
< 32.67) = 0.90 {As the critical value of chi at 21 degrees
of freedom are 11.59 & 32.67}
P(11.59 <
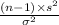 < 32.67) = 0.90
< 32.67) = 0.90
P(
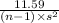 <
<
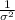 <
<
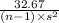 ) = 0.90
) = 0.90
P(
 <
<
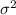 <
<
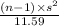 ) = 0.90
) = 0.90
90% confidence interval for
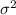 = [
= [
 ,
,
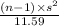 ]
]
= [
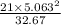 ,
,
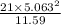 ]
]
= [16.48 , 46.45]
90% confidence interval for
 = [
= [
 ,
,
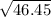 ]
]
= [4.06 , 6.82]
Therefore, a 90% confidence interval for the standard deviation of the fracture toughness distribution is [4.06, 6.82].