Question

a certain plane parallel capacitor stores energy E when the plates have a charge Q on each plate. Then distance between the plates is double. In order to store triply as much energy, how much charge should it have in its plates

Answer 1

`Q'=√(6)Q`

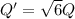
Step-by-step explanation:

You have that a parallel plate capacitor has a total energy of E when the distance between the plates is d and the charge on each plate is Q.

You take into account the following formula for the stored energy in the capacitor:

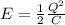`E=(1)/(2)(Q^2)/(C)` (1)

The capacitance C of the parallel plate capacitor is given by the following formula is:

`C=\epsilon_o(A)/(d)` (2)

A: area of the plates

ε0: dielectric permittivity of vacuum

You replace the expression (2) into the equation (1):

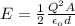`E=(1)/(2)(Q^2A)/(\epsilon_o d)` (3)

the previous formula is the expression for the total energy stored for the given parameters A, d and Q.

If the distance between the plates is twice and it is required that the energy is three times the initial energy, to find the value of the charge you use the equation (3):

`E'=(1)/(2)(Q'^2A)/(\epsilon_o d')` (4)

d' = 2d

E' = 3E

Q': required charge

You replace the values of d' and E' in the equation (4) and then divide the result with the equation (3):

`3E=(1)/(2)(Q'^2A)/(\epsilon_o(2d))=(1)/(4)(Q'^2A)/(\epsilon_od)\\\\(3E)/(E)=(1/4(Q'^2A)/(\epsilon_od))/(1/2(Q^2A)/(\epsilon_o d))\\\\3=(1)/(2)(Q'^2)/(Q^2)`

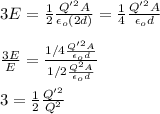
Finally, you solve for Q':

`3=(1)/(2)(Q'^2)/(Q^2)\\\\Q'=√(6)Q`

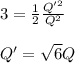
Then, the required charge is √6Q , to obtain three times the initial energy E, when the distance between plates is doubled.