Question

The lengths of adult males' hands are normally distributed with mean 190 mm and standard deviation is 7.4 mm. Suppose that 45 individuals are randomly chosen. Round all answers to 4 where possible.

What is the distribution of ¯xx¯? ¯xx¯ ~ N(,)
For the group of 45, find the probability that the average hand length is less than 189.
Find the third quartile for the average adult male hand length for this sample size.
For part b), is the assumption that the distribution is normal necessary?

Answer 1

a. The distribution of the sample means is normal with mean 190 mm and standard deviation 1.1031 mm.

b. The probability that the average hand length is less than 189 is P(M<189)=0.1823.

c. The third quartile for the average adult male hand length for this sample size is M_75=190.7440.

d. The assumption of normality is not necessary as the sampling distribution will tend to have a bell shaped independently of the population distribution.

Explanation:

We have a normal distribution, with mean 190 and standard deviation 7.4.

We take samples of size n=45 from this population.

Then, the sample means will have a distribution with the following parameters:

`\mu_s=\mu=190\\\\ \sigma_s=(\sigma)/(√(n))=(7.4)/(√(45))=(7.4)/(6.7082)=1.1031`

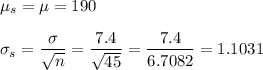
The probability that the sample mean is less than 189 can be calculated as:

`z=(M-\mu)/(\sigma/√(n))=(189-190)/(7.4/√(45))=(-1)/(1.1031)=-0.9065\\\\\\P(M<189)=P(z<-0.9065)=0.1823`

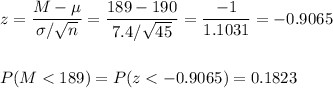
The third quartile represents the value of the sample where 75% of the data is to the left of this value. It means that:

`P(M<M^*)=0.75`

The third quartile corresponds to a z-value of z*=0.6745.

`P(z<z^*)=0.75`

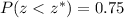
Then, we can calculate the sample mean for the third quartile as:

`M=\mu_s+z^*\sigma_s=190+0.6745\cdot 1.1031=190+0.7440=190.7440`

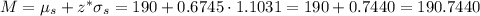
The assumption of normality is not necessary as the sampling distribution will tend to have a bell shaped independently of the population distribution.