Question

The city of Modesto, California needs more water. The town engineer has selected two plans for comparison: a gravity-based plan (divert water from the Sierras and pipe it by gravity to the city) and a pumping plan (pump water from a closer water source to the city). The pumping plant would be built in two stages, with half-capacity installed initially and the other half installed 10 years later.The analysis should assume a 40-year life, 10% interest on the municipal loan used to finance the project, and no salvage value of the project or equipment and the end of its life. Gravity Pumping Initial investment $2.8 million $1.4 millionAdditional investment in year 10 None $200,000Operation and maintenance $10,000/yr $25,000/yr Power cost Average the first 10 years None $50,000/yr Average the next 30 years None $100,000/yr(a) Use an annual cash flow analysis to find out which plan is preferred(b) What is the breakeven investment cost in year 10 to make these two projects equally preferable?

Answer 1

a pumping plan (pump water from a closer water source to the city) is prefered.

the breakeven investment cost in year 10 is $1311018. 802 in order to make these two projects equally preferable

Step-by-step explanation:

From the given information; we are to :

(a) Use an annual cash flow analysis to find out which plan is preferred

(b) What is the breakeven investment cost in year 10 to make these two projects equally preferable?

The two plans selected by the engineer are:

a gravity-based plan (divert water from the Sierras and pipe it by gravity to the city)

a pumping plan (pump water from a closer water source to the city).

In order to achieve that; let's find out the Present Value for each plan.

The Present Value (PV) of cost related to a gravity-based plan is:

`PV = 2800000 +1000 a_(40) _(\urcorner)` at 10%

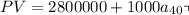`PV = 2800000 +97790.50`

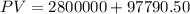
PV = $2897790.5

The Present Value (PV) of cost related to a pumping plan

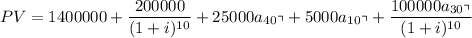`PV = 1400000+ (200000)/((1+i)^(10))+ 25000 a_(40)_(\urcorner)+5000 a_(10)_(\urcorner) + (100000 a_(30) _(\urcorner))/((1+i)^(10))` at 10%

PV = 1400000 + 77108.66 + 244476.27 + 307228.36+363448.36

PV = $2392261.65

Thus; we consider the PV with lower value in order to determine which plan is prefered.

Thus; a pumping plan (pump water from a closer water source to the city) is prefered.

(b).

What is the breakeven investment cost in year 10 to make these two projects equally preferable

Let assume that I = the break even investment cost in year 10 for the prefered pumping plan.

Then;

$2897790.5 = $2392261.65 + (I/(1+i)¹⁰) at 10%

$2897790.5 - $2392261.65 = (I/(1+i)¹⁰) at 10%

$505528.85 = (I/(1+i)¹⁰) at 10%

0.3856 I = 505528.85

I = 505528.85/0.3856

I = $1311018.802

Thus; the breakeven investment cost in year 10 is $1311018.802 in order to make these two projects equally preferable