Answer:
the density of the electrum is 14.30 g/cm³
Step-by-step explanation:
Given that:
The equilibrium fraction of lattice sites that are vacant in electrum =

Number of vacant atoms =
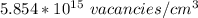
the atomic mass of the electrum = 146.08 g/mol
Avogadro's number =
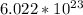
The Number of vacant atoms = Fraction of lattice sites × Total number of sites(N)
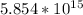 =
=
 × Total number of sites(N)
× Total number of sites(N)
Total number of sites (N) =
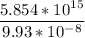
Total number of sites (N) =
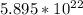
From the expression of the total number of sites; we can determine the density of the electrum;
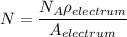
where ;
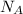 = Avogadro's Number
= Avogadro's Number
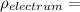 density of the electrum
density of the electrum
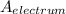 = Atomic mass
= Atomic mass
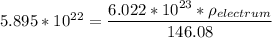
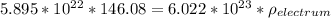
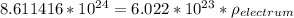
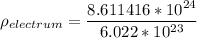
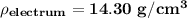
Thus; the density of the electrum is 14.30 g/cm³