Question

A random sample of the price of gasoline from 40 gas stations in a region gives an average price of $3.69 and sample standard deviation 0.25$. Construct a 95% Confidence Interval for the mean price of regular gasoline in that region A. (3.61, 3.77) B. (3.09, 4.29) C. (2.79, 4.59) D. (3.39, 3.99)

Answer 1

95% Confidence Interval for the mean price of regular gasoline in that region

(3.61005, 3.76995)

Explanation:

Step(i):-

Given sample size 'n' =40

mean of the sample x⁻ = 3.69 $

standard deviation of the sample "s' = 0.25 $

We will use students 't' distribution

degrees of freedom

ν = n-1 = 40-1 =39

`t_(39,0.05) = 2.0227`

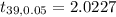
Step(ii):-

95% Confidence Interval for the mean price of regular gasoline in that region

`(x^(-) - t_(\alpha ) (S)/(√(n) ) , (x^(-) + t_(\alpha ) (S)/(√(n) ))`

`(3.69 - 2.0227 (0.25)/(√(40) ) , 3.69 + 2.0227 (0.25)/(√(40) ))`

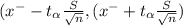
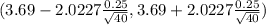
(3.69 - 0.07995 , 3.69 + 0.07995)

(3.61005, 3.76995)

Final answer:-

95% Confidence Interval for the mean price of regular gasoline in that region

(3.61005, 3.76995)