Question

The electric field strength is 5.50×104 N/C inside a parallel-plate capacitor with a 2.30 mm spacing. A proton is released from rest at the positive plate.What is the proton's speed when it reaches the negative plate?

Answer 1

v = 1.09*10^5 m/s

Step-by-step explanation:

In order to calculate the speed of the proton when it reaches the negative plate, you first calculate the acceleration of the proton, produced by the electric force.

You use the second Newton law:

`F_e=qE=ma` (1)

q: charge of the proton = 1.6*10^-19 C

m: mass of the proton = 1.67*10^-27 kg

E: magnitude of the electric field between the plates = 5.50*10^4N/C

You solve for the acceleration a in the equation (1):

`a=(qE)/(m)=((1.6*10^(-19)C)(5.50*10^4N/C))/(1.67*10^(-27)kg)=5.26*10^(12)(m)/(s^2)`

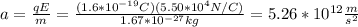
Next, you use the following formula to find the final speed of the proton:

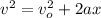`v^2=v_o^2+2ax` (2)

v: final speed of the proton = ?

vo: initial speed of the proton = 0m/s

x: distance traveled by the proton = 2.30mm/2 = 1.15mm = 1.15*10^-3m

You replace the values of all parameters in the equation (2):

`v=√(2ax)=\sqrt{2(5.26*10^(12)m/s^2)(1.15*10^(-3)m)}=1.09*10^5(m)/(s)`

The speed of the proton when it reaches the negative plate is 1.09*10^5 m/s