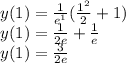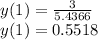Question

Write the value of y(1) if y is the solution of e^t dy/dt+e^ty=t, y(0)=1, round your answer to four digits after the decimal sign

Answer 1

`y(1) = 0.5518`

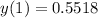
Explanation:

Given the differential equation
`e^(t) (dy)/(dt) +e^(t)y = t`

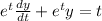
From the equation;

`e^(t) ((dy)/(dt) +y) = t\\(dy)/(dt) +y = (t)/(e^(t)) \\`

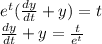
The resulting equation is a first order differential equation in the form

dy/dt + p(t)y = q(t)

The solution to the DE will be in the form yI =
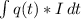`\int\limits q(t)*I\, dt` where I is the integrating factor expressed as
`I = e^(\int\limits p(t) \, dt )`

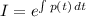
From the DE above p(t ) = 1 and q(t) =
`(t)/(e^(t) )`

`I = e^(\int\limits1 \, dt )\\I = e^(t )\\`

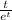
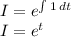
The solution to the DE will become

`y e^(t ) = \int\limits e^(t ) *(t)/(e^(t ) ) \, dt\\y e^(t ) = \int\limits{t} \, dt \\y e^(t ) = (t^(2) )/(2) + C`

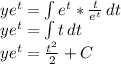
If y(0) = 1 then;

`1 e^(0 ) = (0^(2) )/(2) + C\\1 = C`

`y e^(t ) = (t^(2) )/(2) + 1\\y(t) = (1)/(e^(t ) ) ((t^(2) )/(2) + 1)`

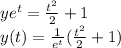
The value of y(1) will be expressed as;

`y(1) = (1)/(e^(1) ) ((1^(2) )/(2) + 1)\\y(1) = (1)/(2e)+(1)/(e)\\ y(1) = (3)/(2e)`

`y(1) = (3)/(5.4366) \\y(1) = 0.5518`