Question

A spherical shell is rolling without slipping at constant speed on a level floor. What percentage of the shell's total kinetic energy is translational kinetic energy

Answer 1

41.667 per cent of the total kinetic energy is translational kinetic energy.

Step-by-step explanation:

As the spherical shell is rolling without slipping at constant speed, the system can be considered as conservative due to the absence of non-conservative forces (i.e. drag, friction) and energy equation can be expressed only by the Principle of Energy Conservation, whose total energy is equal to the sum of rotational and translational kinetic energies. That is to say:

`E = K_(t) + K_(r)`

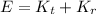
Where:

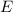`E` - Total energy, measured in joules.

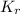`K_(r)` - Rotational kinetic energy, measured in joules.

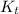`K_(t)` - Translational kinetic energy, measured in joules.

The spherical shell can be considered as a rigid body, since there is no information of any deformation due to the motion. Then, rotational and translational components of kinetic energy are described by the following equations:

Rotational kinetic energy

`K_(r) = (1)/(2)\cdot I_(g)\cdot \omega^(2)`

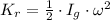
Translational kinetic energy

`K_(t) = (1)/(2)\cdot m \cdot R^(2)\cdot \omega^(2)`

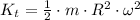
Where:

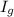`I_(g)` - Moment of inertia of the spherical shell with respect to its center of mass, measured in
`kg\cdot m^(2)`.

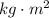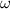`\omega` - Angular speed of the spherical shell, measured in radians per second.

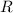`R` - Radius of the spherical shell, measured in meters.

After replacing each component and simplifying algebraically, the total energy of the spherical shell is equal to:

`E = (1)/(2)\cdot (I_(g) + m\cdot R^(2))\cdot \omega^(2)`

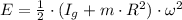
In addition, the moment of inertia of a spherical shell is equal to:

`I_(g) = (2)/(3)\cdot m\cdot R^(2)`

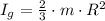
Then, total energy is reduced to this expression:

`E = (5)/(6)\cdot m \cdot R^(2)\cdot \omega^(2)`

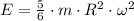
The fraction of the total kinetic energy that is translational in percentage is given by the following expression:

`\%K_(t) = (K_(t))/(E)* 100\,\%`

`\%K_(t) = ((1)/(2)\cdot m \cdot R^(2)\cdot \omega^(2) )/((5)/(6)\cdot m \cdot R^(2)\cdot \omega^(2) ) * 100\,\%`

`\%K_(t) = (5)/(12)* 100\,\%`

`\%K_(t) = 41.667\,\%`

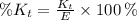
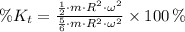
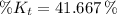
41.667 per cent of the total kinetic energy is translational kinetic energy.