Question

The aorta pumps blood away from the heart at about 40 cm/s and has a radius of about 1.0 cm. It then branches into many capillaries, each with a radius of about 5 x 10−4 cm carrying blood at a speed of 0.10 cm/s.

How many capillaries are there?

Answer 1

n = 1.6*10^9 capillaries

Step-by-step explanation:

In order to calculate the number of capillaries, you take into account that the following relation must be accomplished:

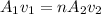`A_1v_1=nA_2v_2` (1)

A1: area of the aorta

v1: speed of the blood in the aorta = 40cm/s

n: number of capillaries = ?

A2: area of each capillary

v2: speed of the blood in each capillary

For the calculation of A1 and A2 you use the formula for the cross sectional area of a cylinder, that is, the area of a circle:

`A=\pi r^2\\\\A_1=\pi r_1^2=\pi(1.0cm)^2=3.1415 cm^2\\\\A_2=\pi r_2^2=\pi (5*10^(-4)cm)^2=7.85*10^(-7)cm^2`

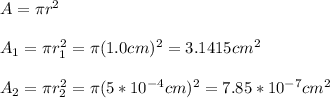
Where you have used the values of the radius for the aorta and the capillaries.

Next, you solve the equation (1) for n, and replace the values of all parameters:

`n=(A_1v_1)/(A_2v_2)=((3.1415cm^2)(40cm/s))/((7.85*10^(-7)cm^2)(0.10cm/s))=1.6*10^9`

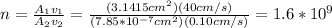
Then, the number of capillaries is 1.6*10^9