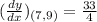Question

Find an equation of the tangent line to the curve at the given point.x2+2xy−y2+x=101, (7,9) (hyperbola)

Answer 1

The equation of the tangent line of the given curve

`(dy)/(dx) = (- (2x +2y +1))/(( 2 x - 2 y))`

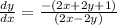
The tangent of the given curve at the point

`((dy)/(dx))_((7,9)) = (33)/(4)`

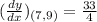
Explanation:

Explanation :-

Step(i):-

Given equation of the parabola

x²+2xy−y²+x=101 ...(i)

apply derivative Formulas

a)
`(dx^(n) )/(dx) = n x ^(n-1)`

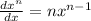
b)
`(d U V )/(dx) = U (dV)/(dx) + V (dU)/(dx)`

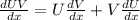
Step(ii):-

Differentiating equation (i) with respective to 'x' , we get

`2 x + 2 ( x (dy)/(dx) + y) - 2 y (dy)/(dx) +1 = 0`

`2 x + 2 x (dy)/(dx) +2 y - 2 y (dy)/(dx) +1 = 0`

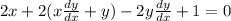
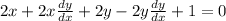
on simplification , we get

`( 2 x - 2 y) (dy)/(dx) = - (2x +2y +1)`

`(dy)/(dx) = (- (2x +2y +1))/(( 2 x - 2 y))`

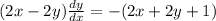
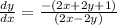
The tangent of the given curve at the point ( 7,9)

`((dy)/(dx))_((7,9)) = (- ((2(7) +2(9) +1)))/(( 2 (7) - 2 (9))`

`((dy)/(dx))_((7,9)) = (- (33))/(( -4) = (33)/(4)`

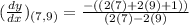
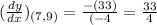
Final answer :-

The equation of the tangent line of the given curve

`(dy)/(dx) = (- (2x +2y +1))/(( 2 x - 2 y))`

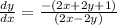
The tangent of the given curve at the point

`((dy)/(dx))_((7,9)) = (33)/(4)`