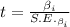Question

To determine if a particular predictor in a regression analysis is statistically significant, which statistic should one interpret

Answer 1

The test statistic used to determine whether a particular predictor in a regression analysis is statistically significant is:

`t=\frac{\beta_(i)}{S.E._{\beta_(i)}}`

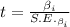
Explanation:

The general form of a regression equation is:

`y=\alpha +\beta_(1)x_(1)+\beta_(2)x_(2)+...+\beta_(n)x_(n)`

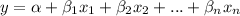
Here,

α = y-intercept

βi = regression coefficients, (i = 1, 2, ..., n)

A regression analysis is performed to determine whether the predictor variables are statistically significant or not.

The output of the regression analysis consists of two tables.

One is the regression output and the other is the ANOVA table.

The regression output table is used to display which predictor variables are statistically significant and which are not.

The test statistic used to determine whether a particular predictor in a regression analysis is statistically significant is:

`t=\frac{\beta_(i)}{S.E._{\beta_(i)}}`

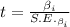
And the ANOVA table displays overall regression analysis.

The F-test statistic is used to for the overall regression analysis.

Thus, the test statistic used to determine whether a particular predictor in a regression analysis is statistically significant is:

`t=\frac{\beta_(i)}{S.E._{\beta_(i)}}`