Question

Refer to the accompanying data set and construct a 90​% confidence interval estimate of the mean pulse rate of adult​ females; then do the same for adult males. Compare the results.

Male/Females
81 82
77 94
53 60
59 66
53 53
60 81
54 78
76 83
52 87
64 53
73 34
57 64
65 83
78 74
79 81
66 66
69 65
94 76
45 61
89 64
71 82
66 80
70 71
74 77
52 88
68 90
56 87
79 91
75 89
62 93
66 68
96 87
60 83
65 81
55 74
57 56
70 101
70 71
83 74
57 77

Answer 1

The required 90% confidence interval for adult males is

`\text {CI} = (64.2, \: 70.6)\\\\`

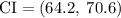
The required 90% confidence interval for adult females is

`\text {CI} = (72, \: 79.2)\\\\`

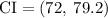
The confidence interval of male and female pulse rates do not overlap since the mean pulse rate of female is way greater than the mean pulse rate of males.

Explanation:

We are given the pulse rates of adult females and adult males and we have to construct the 90% confidence interval of the mean pulse rate for males and females.

Let us first compute the mean and standard deviation of the given pulse rates data.

Using Excel,

=AVERAGE(number1, number2,....)

The mean pulse rate of adult males is found to be

`\bar{x}_(male) = 67.4`

The mean pulse rate of adult females is found to be

`\bar{x}_(female) = 75.6`

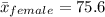
Using Excel,

=STDEV(number1, number2,....)

The standard deviation for adult male pulse rate is found to be

`s_(male) = 11.9`

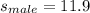
The standard deviation for adult female pulse rate is found to be

`s_(female) = 13.5`

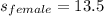
The confidence interval is given by

`$ \text {CI} = \bar{x} \pm t_(\alpha/2)((s)/(√(n) ) ) $\\\\`

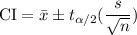
Where
`\bar{x}` is the sample mean, n is the sample size, s is the sample standard deviation and
`t_(\alpha/2)` is the t-score corresponding to a 90% confidence level.

The t-score corresponding to a 90% confidence level is

Significance level = α = 1 - 0.90 = 0.10/2 = 0.05

Degree of freedom = n - 1 = 40 - 1 = 39

From the t-table at α = 0.05 and DoF = 39

t-score = 1.685

The required 90% confidence interval for adult males is

`\text {CI} = 67.4 \pm 1.685\cdot (11.9)/(√(40) ) \\\\\text {CI} = 67.4 \pm 1.685\cdot 1.882\\\\\text {CI} = 67.4 \pm 3.17\\\\\text {CI} = 67.4 - 3.17, \: 67.4 + 3.17\\\\\text {CI} = (64.2, \: 70.6)\\\\`

Therefore, we are 90% confident that the actual mean pulse rate of adult male is within the range of 64.2 to 70.6 bpm

The required 90% confidence interval for adult females is

`\text {CI} = 75.6 \pm 1.685\cdot (13.5)/(√(40) ) \\\\\text {CI} = 75.6 \pm 1.685\cdot 2.1345\\\\\text {CI} = 75.6 \pm 3.60\\\\\text {CI} = 75.6 - 3.60, \: 75.6 + 3.60\\\\\text {CI} = (72, \: 79.2)\\\\`

Therefore, we are 90% confident that the actual mean pulse rate of adult female is within the range of 72 to 79.2 bpm

Comparison:

The confidence interval of male and female pulse rates do not overlap since the mean pulse rate of female is way greater than the mean pulse rate of males.