Question

A triangular plot of land has one side along a straight road measuring 147147 feet. A second side makes a 2323degrees° angle with the​ road, and the third side makes a 2222degrees° angle with the road. How long are the other two​ sides?

Answer 1

81.23 ft and 77.88 ft long

Explanation:

The sum of the internal angles of a triangle is 180 degrees, the missing angle is:

`a+b+c=180\\a+23+22=180\\a=135^o`

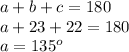
According to the Law of Sines:

`(A)/(sin(a))= (B)/(sin(b))= (C)/(sin(c))`

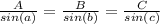
Let A be the side that is 147 feet long, the length of the other two sides are:

`(A)/(sin(a))= (B)/(sin(b))\\B=(sin(23)*147)/(sin(135))\\B=81.23\ ft\\\\(A)/(sin(a))= (C)/(sin(c))\\C=(sin(22)*147)/(sin(135))\\C=77.88\ ft`

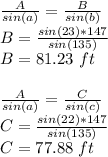
The other two sides are 81.23 ft and 77.88 ft long