Answer:
(a) The odds for and against E are (8:1) and (1:8) respectively.
(b) The odds for and against E are (7:2) and (2:7) respectively.
(c) The odds for and against E are (59:41) and (41:59) respectively.
(d) The odds for and against E are (71:29) and (29:71) respectively.
Explanation:
The formula for the odds for an events E and against and event E are:
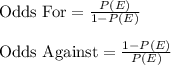
(a)
The probability of the event E is:
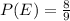
Compute the odds for and against E as follows:
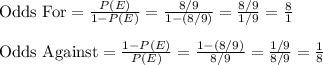
Thus, the odds for and against E are (8:1) and (1:8) respectively.
(b)
The probability of the event E is:

Compute the odds for and against E as follows:
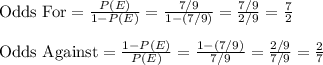
Thus, the odds for and against E are (7:2) and (2:7) respectively.
(c)
The probability of the event E is:
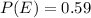
Compute the odds for and against E as follows:

Thus, the odds for and against E are (59:41) and (41:59) respectively.
(d)
The probability of the event E is:
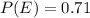
Compute the odds for and against E as follows:

Thus, the odds for and against E are (71:29) and (29:71) respectively.