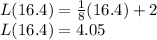Question

Use linear approximation, i.e. the tangent line, to approximate √16.4 as follows: Let f(x)=√x. Find the equation of the tangent line

Answer 1

`L(x)=(1)/(8)x+2\\ L(16.4)=4.05`

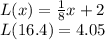
Explanation:

The equation for a tangent line of f(x) in the point (a,f(a)) can be calculated as:

L(x) = f(a) + f'(a)(x-a)

Where L(x) is also call a linear approximation and f'(a) is the value of the derivative of f(x) in (a,f(a)).

So, the derivative of f(x) is:

`f(x)=√(x) \\f'(x)=(1)/(2√(x) )`

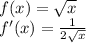
Then, to find the linear approximation we are going to use the point (16, f(16)). So a is 16 and f(a) and f'(a) are calculated as:

`f(16)=√(16)=4\\f'(16)=(1)/(2√(16) )=(1)/(8)`

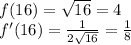
Then, replacing the values, we get that the equation of the tangent line in (16,4) is:

`L(x)=4+(1)/(8)(x-16)\\L(x) = (1)/(8)x+2`

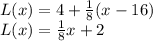
Finally, the approximation for
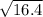`√(16.4)` is:

`L(16.4)=(1)/(8)(16.4)+2\\ L(16.4)=4.05`