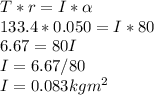Question

A bucket of water with total mass 23 kg is attached to a rope, which in turn is wound around a 0.050-m radius pulley at the top of a well. The bucket is raised to the top of the well and released from rest. The bucket is falling for 2 s and has a speed of 8.0 m/s upon hitting the water surface in the well. What is the moment of inertia of the pulley?

Answer 1

`I = 0.083 kg m^2`

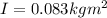
Step-by-step explanation:

Mass of the bucket, m = 23 kg

Radius of the pulley, r = 0.050 m

The bucket is released from rest, u = 0 m/s

The time taken to fall, t = 2 s

Speed, v = 8.0 m/s

Moment of Inertia of the pulley, I = ?

Using the equation of motion:

v = u + at

8 = 0 + 2a

a = 8/2

a = 4 m/s²

The relationship between the linear and angular accelerations is given by the equation:

`a = \alpha r`

Angular acceleration,
`\alpha = a/r`

`\alpha = 4/0.050\\\alpha = 80 rad/s^2`

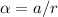
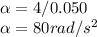
Since the bucket is falling, it can be modeled by the equation:

mg - T = ma

T = mg - ma = m(g-a)

T = 23(9.8 - 4)

The tension, T = 133.4 N

The equation for the pulley can be modeled by:

`T* r = I * \alpha\\133.4 * 0.050 = I * 80\\6.67 = 80 I\\I = 6.67/80\\I = 0.083 kg m^2`