Answer:
See step-by-step explanation.
Explanation:
Part 1: Use the law of cosines to find the measure of angle B:
Law of cosines: c^2 = a2 + b2 − 2ab cos(C)
In this case, you're finding b, so b is basically c.
b^2 = a2 + c2 − 2ab cos(b)
b=21 a=22 c=16 (just for now)
21^2 = 22^2+16^2- 2(22)(16) cos (b)
441= 484 + 256 - 704 cos(b)
Measure of angle B= 64.8673
Part 2: Use the law of sines to find the measure of angle C
 =
=
 =
=
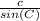
Using angle b and sides b and c: 43.6121
21/ sin ( 64.8673) = 16/ sin(C)
Measure of angle C = 43.6121
Part 3: Find the measure of angle A
1. The angles in a triangle add up 180.
m<A+m<B+m<C=180
m<A+64.8673 + 43.6121 =180
Measure of angle A=71.5206
Page 2
Part 1: Find the measure of angle B
The angles in a triangle add up 180.
m<A+m<B+m<C=180.
42+ m<B+83=180
Measure of angle B= 55 degrees
Part 2: Use the law of sines to find the length of side a
 =
=
 =
=
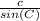
Length of side a =
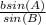 =
=
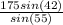
The length of side a: 142.95
Part 3: Use any method to find the length of side c.
Method= brainpower
aka law of sines:
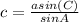 =
=
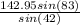
c= 212.043
The length of side c: 212.043