Question

A wave with a frequency of 1200 Hz propagates along a wire that is under a tension of 800 N. Its wavelength is 39.1 cm. What will be the wavelength if the tension is decreased to 600 N and the frequency is kept constant

Answer 1

The wavelength will be 33.9 cm

Step-by-step explanation:

Given;

frequency of the wave, F = 1200 Hz

Tension on the wire, T = 800 N

wavelength, λ = 39.1 cm

`F = \frac{ \sqrt{(T)/(\mu) }}{\lambda}`

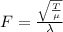
Where;

F is the frequency of the wave

T is tension on the string

μ is mass per unit length of the string

λ is wavelength

`\sqrt{(T)/(\mu) } = F \lambda\\\\(T)/(\mu) = F^2\lambda^2\\\\\mu = (T)/(F^2\lambda^2) \\\\(T_1)/(F^2\lambda _1^2) = (T_2)/(F^2\lambda _2^2) \\\\(T_1)/(\lambda _1^2) = (T_2)/(\lambda _2^2)\\\\T_1 \lambda _2^2 = T_2\lambda _1^2\\\\`

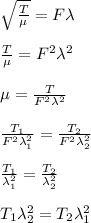
when the tension is decreased to 600 N, that is T₂ = 600 N

`T_1 \lambda _2^2 = T_2\lambda _1^2\\\\\lambda _2^2 = (T_2\lambda _1^2)/(T_1) \\\\\lambda _2 = \sqrt{(T_2\lambda _1^2)/(T_1)} \\\\\lambda _2 = \sqrt{(600* 0.391^2)/(800)}\\\\\lambda _2 = √(0.11466) \\\\\lambda _2 =0.339 \ m\\\\\lambda _2 =33.9 \ cm`

Therefore, the wavelength will be 33.9 cm