Answer:
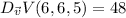
Explanation:
You have the following potential function:
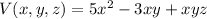 (1)
(1)
To find the rate of change of the potential at the point P(6,6,5) in the direction of v = i + j - k, you use the following formula:
 (2)
(2)
First, you calculate the gradient of V:

Next, you replace in the equation (2):
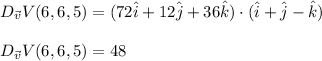
Then, the rate of change of the potential at the point P(6,6,5) in the direction of v, is 48.