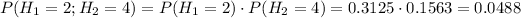Question

a coin will be tossed 10 times. Find the chance that there will be exactly 2 heads among the first five tosses and exactly 4 heads among the last 5 tosses

Answer 1

The chance that there will be exactly 2 heads among the first five tosses and exactly 4 heads among the last 5 tosses is P=0.0488.

Explanation:

To solve this problem we divide the tossing in two: the first 5 tosses and the last 5 tosses.

Both heads and tails have an individual probability p=0.5.

Then, both group of five tosses have the same binomial distribution: n=5, p=0.5.

The probability that k heads are in the sample is:

`P(x=k)=\dbinom{n}{k}p^k(1-p)^(n-k)=\dbinom{5}{k}\cdot0.5^k\cdot0.5^(5-k)`

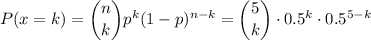
Then, the probability that exactly 2 heads are among the first five tosses can be calculated as:

`P(x=2)=\dbinom{5}{2}\cdot0.5^(2)\cdot0.5^(3)=10\cdot0.25\cdot0.125=0.3125\\\\\\`

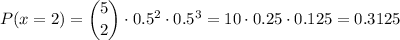
For the last five tosses, the probability that are exactly 4 heads is:

`P(x=4)=\dbinom{5}{4}\cdot0.5^(4)\cdot0.5^(1)=5\cdot0.0625\cdot0.5=0.1563\\\\\\`

Then, the probability that there will be exactly 2 heads among the first five tosses and exactly 4 heads among the last 5 tosses can be calculated multypling the probabilities of these two independent events:

`P(H_1=2;H_2=4)=P(H_1=2)\cdot P(H_2=4)=0.3125\cdot0.1563=0.0488`