Question

4 years ago, the population of a city was "x" inhabitant. 2 years later, two years ago, the population of this same city was 81,000 and today it is 65,610. Using this data, finds the population of four years ago

Answer 1

59049.

Explanation:

It is given that, 2 years later, two years ago, the population of this same city was 81,000 and today it is 65,610.

So, graph passing through (2,81000) and (-2,65610).

The general exponential function is

`y=ab^x`

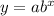
where, a is initial value or present year population and b is growth factor.

Since graph passing through (2,81000) and (-2,65610), therefore the above equation must be satisfied by these points.

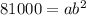`81000=ab^2` ...(1)

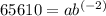`65610=ab^((-2))` ...(2)

Multiplying (1) and (2), we get

`81000* 65610=ab^2* ab^(-2)`

`5314410000=a^2`

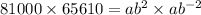
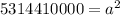
Taking square root on both sides.

`72900=a`

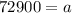
Substitute a=72900 in (1).

`81000=72900b^2`

`(81000)/(72900)=b^2`

`(10)/(9)=b^2`

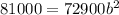
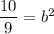
Taking square root on both sides.

`(√(10))/(3)=a`

So, the population function is

`y=72900\left((√(10))/(3)\right)^x`

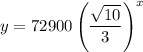
Substitute x=-4 in the above equation, to find the population of four years ago.

`y=72900\left((√(10))/(3)\right)^(-4)`

`y=72900(0.81)`

`y=59049`

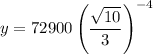
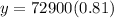
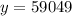
Therefore, the population of four years ago is 59049.