Question

A laser beam of wavelength 720 nm shines through a diffraction grating that has 750 lines/mm and observed on a screen 1.4 m behind the grating. For the steps and strategies involved in solving a similar problem, you may view a Video Tutor Solution. Part A How many bright fringes can be observed on a screen

Answer 1

m_max = 5

Step-by-step explanation:

In order to calculate the number of bright fringes on the screen, you first take into account the diffraction grating equation:

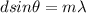`dsin\theta=m\lambda` (1)

d: distance between slits

m: order of a bright fringe

λ: wavelength of light = 720nm = 720*10^-9m

θ: angle between the normal to the grating and the mth bright fringe

The maximum number of fringes is obtained when the angle θ is a maximum, that is, for θ=90°

The distance between slits is calculated by using the following formula:

`d=(1)/(N)`

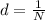
N: number of slits per meter = 750 lines/mm

`d=(1)/(750lines/mm)=1.333*10^(-3)mm=1.333*10^(-6)m`

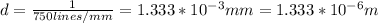
You solve for m in the equation (1)m, and replace the values of d and θ for the maximum number of bright fringes over the normal to the screen.

`m=(dsin\theta)/(\lambda)\\\\m=((1.333*10^(-6)m)sin90\°)/(720*10^(-9)m)=1.85`

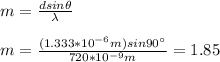
The maximum number of bright fringes is an integer, then you approximate m = 2. This means that there are two bright fringes above the central peak.

The total number of fringes is twice the previous value of m plus the central peak:

`m_(max)=2m+1=2(2)+1=5`

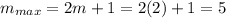
There are 5 bright fringes in the diffraction pattern