Question

From 1960 to 2010, a certain money stock measure was growing at the rate of approximately 43e(1/2)x billion dollars per decade, where x is the number of decades since 1950. Find the total increase in the money stock measure from 1960 to 2010. (Round your answer to the nearest billion dollars.)

Answer 1

1222 billion dollars.

Explanation:

To find the total increase from 1960 to 2010, we need to find the growth of each decade and sum them all:

In the period 1960-1970, we have x = 1, and the growth is:

`y(1) = 43e(1/2) = 70.895`

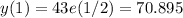
In the period 1970-1980, we have x = 2, and the growth is:

`y(2) = 43e(2/2) = 116.8861`

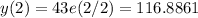
The growth in the following 3 periods are:

`y(3) = 43e(3/2) =192.7126`

`y(4) = 43e(4/2) = 317.7294`

`y(5) = 43e(5/2) =523.8472`

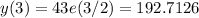
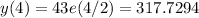
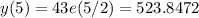
So the total growth in the period 1960 - 2010 is:

`Total = y(1) + y(2) + y(3) + y(4) + y(5)`

`Total = 70.895 + 116.8861+192.726+317.7294+523.8472`

`Total = 1222.08\ billion\ dollars`

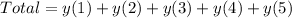
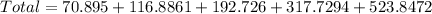
Rounding to the nearest billion dollars, we have a total of 1222 billion dollars.