Question

In a survey of 1309 people, 825 people said they voted in a recent presidential election. Voting records show that 60% of eligible voters actually did vote. Given that 60% of eligible voters actually did vote,

(a) find the probability that among 1309 randomly selected voters, at least 825 actually did vote.
(b) What do the results from part (a) suggest?

Answer 1

a) P(X>825)

b) This low value of probability of the sample outcome (as 825 voters actually did vote) suggests that the 60% proportion may not be the true population proportion of eligible voters that actually did vote.

Explanation:

We know a priori that 60% of the eligible voters did vote.

From this proportion and a sample size n=1309, we can construct a normal distribution probabilty, that is the approximation of the binomial distribution for large samples.

Its mean and standard deviation are:

`\mu=n\cdot p=1309\cdot 0.6=785.4\\\\\sigma =√(np(1-p))=√(1309\cdot 0.6\cdot 0.4)=√(314.16)=17.7`

Now, we have to calculate the probabilty that, in the sample of 1309 voters, at least 825 actually did vote. This is P(X>825).

This can be calculated using the z-score for X=825 for the sampling distribution we calculated prerviously:

`z=(X-\mu)/(\sigma)=(825-785.4)/(17.7)=(39.6)/(17.7)=2.24\\\\\\P(X>825)=P(z>2.24)=0.0126`

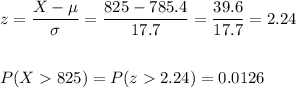
This low value of probability of the sample outcome (as 825 voters actually did vote) suggests that the 60% proportion may not be the true population proportion of eligible voters that actually did vote.