Question

Suppose you pay a dollar to roll two dice. if you roll 5 or a 6 you Get your dollar back +2 more just like it the goal will be to find the amount of money you can expect to win or lose if you play this game 100 times. How many times would you win? how many times would you lose?

Answer 1

(a)$67

(b)You are expected to win 56 Times

(c)You are expected to lose 44 Times

Explanation:

The sample space for the event of rolling two dice is presented below

`(1,1), (2,1), (3,1), (4,1), (5,1), (6,1)\\(1,2), (2,2), (3,2), (4,2), (5,2), (6,2)\\(1,3), (2,3), (3,3), (4,3), (5,3), (6,3)\\(1,4), (2,4), (3,4), (4,4), (5,4), (6,4)\\(1,5), (2,5), (3,5), (4,5), (5,5), (6,5)\\(1,6), (2,6), (3,6), (4,6), (5,6), (6,6)`

Total number of outcomes =36

The event of rolling a 5 or a 6 are:

`(5,1), (6,1)\\ (5,2), (6,2)\\( (5,3), (6,3)\\ (5,4), (6,4)\\(1,5), (2,5), (3,5), (4,5), (5,5), (6,5)\\(1,6), (2,6), (3,6), (4,6), (5,6), (6,6)`

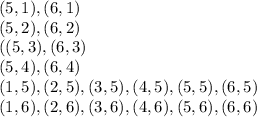
Number of outcomes =20

Therefore:

P(rolling a 5 or a 6)
`=(20)/(36)`

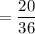
The probability distribution of this event is given as follows.

`\left|\begin{array}c$Amount Won(x)&-\$1&\$2\\&\\P(x)&(16)/(36)&(20)/(36)\end{array}\right|`

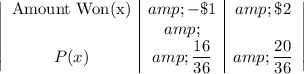
First, we determine the expected Value of this event.

Expected Value

`=(-\$1* (16)/(36))+ (\$2* (20)/(36))\\=\$0.67`

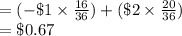
Therefore, if the game is played 100 times,

Expected Profit =$0.67 X 100 =$67

If you play the game 100 times, you can expect to win $67.

(b)

Probability of Winning
`=(20)/(36)`

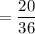
If the game is played 100 times

Number of times expected to win

`=(20)/(36) * 100\\=56$ times`

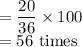
Therefore, number of times expected to loose

= 100-56

=44 times