Question

Adam must fly home to city A from a business meeting in city B. One flight option flies directly to city A from​ B, a distance of about 456.2456.2 miles. A second flight option flies first to city C and then connects to A. The bearing from B to C is N2929degrees°​E, and the bearing from B to A is N59.759.7degrees°E. The bearing from A to B is S59.759.7degrees°​W, and the bearing from A to C is N78.978.9degrees°W. How many more frequent flyer miles will Adam receive if he takes the connecting flight rather than the direct​ flight? Adam would receive nothing more frequent flyer miles.

Answer 1

105.6 miles

Explanation:

• The bearing from B to C is N29°​E
• The bearing from B to A is N59.7°E.
• The bearing from A to B is S59.7°​W
• The bearing from A to C is N78.9°W.
• Distance from A to B = 456.2 miles

In the diagram

The angle at B = 59.7°-29°=30.7°

The angle at A =180°-(78.9°+59.7°)=41.4°

Using the sum of angles in a triangle, Angle C = 107.9°

Applying the Law of Sines

`(b)/(\sin B)=(c)/(\sin C)\\b=(c)/(\sin C) * \sin B\\\\=(456.2)/(\sin 107.9^\circ) * \sin 30.7^\circ\\\\AC=b=244.76$ miles`

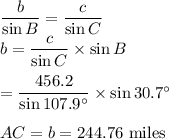
Similarly

`(a)/(\sin A)=(c)/(\sin C)\\a=(c)/(\sin C) * \sin A\\\\=(456.2)/(\sin 107.9^\circ) * \sin 41.4^\circ\\\\BC=a=317.04$ miles`

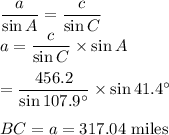
Therefore:

AC+BC=244.76+317.04 =561.8 miles

Difference

561.8 - 456.2 =105.6 miles

Therefore, Adam would receive 105.6 miles more frequent flyer miles.