Answer:
The mean of 50 mg/liter is not inside the 99% interval, so there is not enough evidence to support their claim.
Explanation:
First we need to find the z-value for a confidence of 99%
The value of alpha for a 99% confidence is:
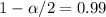
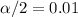

Looking in the z-table, we have z = 2.575.
Now we can find the standard error of the mean:
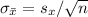
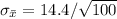
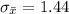
Finding the 99% confidence interval, we have:
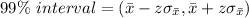

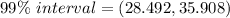
The mean of 50 mg/liter is not inside the 99% interval, so there is not enough evidence to support their claim.