Question

An urn contains 11 balls, 3 white, 3 red, and 5 blue balls. Take out two balls at random, without replacement. You win $1 for each red ball you select and lose a $1 for each white ball you select. Let X be the random variable that notes the amount you win. Find the probability mass function (p.m.f.) of X.

Answer 1

Answer with explanation:

Given: An urn contains 11 balls, 3 white, 3 red, and 5 blue balls.

You win $1 for each red ball you select and lose a $1 for each white ball you select.

Let X be the number of times you win.

The total number of ways to select 2 balls (order does not matter) =

The number of ways so that two balls are white (and
`X=-2):^3C_2=3`

`P(X=-2)=(3)/(55)`

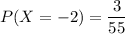
The number of ways so that two balls are red (and
`X=2):^3C_2=3`

`P(X=2)=(3)/(55)`

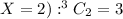
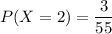
The number of ways so that one ball is red, one is white (and
`X=0):^3C_1*^3C_1=9`

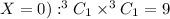
The number of ways so that two balls are blue (and
`X=0` ):
`^5C_2=(5 \cdot 4) / 2=10`

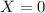i.e.
`P(X=0)=(10+9)/(55)=(19)/(55)`

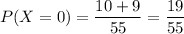
The number of ways so that one ball is blue, one is white (and
`X=-1` ):
`^5C_1*^3C_1=15`

`P(X=-1)=(15)/(55) =(3)/(11)`

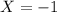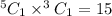
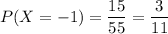
The number of ways so that one ball is blue, one is red (and
`X=1` ):
`^5C_1*^3C_1=15`

`P(X=1)=(15)/(55) =(3)/(11)`

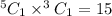
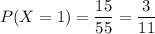
Thus, the probability mass function (p.m.f.) of X would be ( in attachment) :