Question

Flank wear data were collected in a series of turning tests using a coated carbide tool on hardened alloy steel at a feed of 0.30 mm/rev and a depth of 4.0 mm. At a speed of 100 m/min, flank wear = 0.12 mm at 1 min, 0.27 mm at 5 min, 0.45 mm at 11 min, 0.58 mm at 15 min, 0.73 at 20 min, and 0.97 mm at 25 min. At a speed of 155 m/min, flank wear = 0.22 mm at 1 min, 0.47 mm at 5 min, 0.70 mm at 9 min, 0.80 mm at 11 min, and 0.99 mm at 13 min. The last value in each case is when final tool failure occurred.(a) On a single piece of linear graph paper, plot flank wear as a function of time for both speeds. You may use Excel to help yourself to plot the curve. Using 0.75 mm of flank wear as the criterion of tool failure, determine the tool lives for the two cutting speeds.(b) Calculate the values of n and C in the Taylor equation solving simultaneous equations.

Answer 1

A) n = 0.6143, c ≈ 640m/min

B) n = 0.6143 , c = 637.53m/min

Step-by-step explanation:

using the given data

A) A plot of flank wear as a function of time and also A plot for tool when

Flank wear is 0.75 and cutting edge speed is 100m/min, Time of cutting edge is said to be 20.4 min also for cutting edge speed of 155m/min , time for cutting edge is 10 min

is attached below

calculate for the constant N from the second plot

note : the slope will be negative because cutting speed decreases as time of cutting increase

V1 = 100m/min , V2 = 155m/min, T1 = 20.4 min, T2 = 10 min

= - N =
`(In(V2) - In(V1))/(In(T2)-ln(T1))`

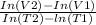
therefore - N =
`(5.043 - 4.605)/(2.302 -3.015)`

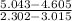
= - 0.6143

THEREFORE ( N ) = 0.6143

Determine for the constant C from the second plot as well

note : C is the intercept on the cutting speed axis in 1 min tool life

connecting the two points with a line and extend it to touch the cutting speed axis and measure the value at that point

hence C ≈ 640m/min

B) Calculate the values of N and C in the Taylor equation solving simultaneous equations

using the above cutting speed and time of cutting values we can find the constant N via Taylor tool life equation

Taylor tool life equation = vT = C ------------- equation 1

cutting speed = v = 100m/min and 155m/min

tool life = T = 20.4 min and 10 min

also constant n and c are obtained from the previous plot

back to taylor tool life equation = 100 * 20.4 = C

therefore C = (100)(20.4)^n ---------------- equation 2

also using the second values of v and T

taylor tool life equation = 155 * 10 = C

therefore C = ( 155 )(10)^n ----------------- equation 3

Equate equation 2 and equation 3 and solve simultaneously

(100)(20.4)^n = (155)(10)^n

To find N

take natural log of both sides of the equation

= In ((100)(20.4)^n) = In((155)(10)^n)

= In (100) + nIn(20.4) = In(155) + nIn(10)^n

= n(3.0155) - n (2.3026) = 5.043 - 4.605

= 0.7129 n = 0.438

therefore n = 0.6143

To find C

substitute 0.6143 for n in equation 2

C = (100)(20.4) ^ 0.6143

C = 637.53 m/min

Attached are the two plots for solution A