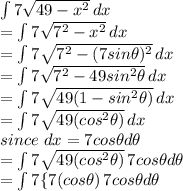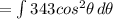Question

Evaluate the following integral using trigonometric substitution.

Integral from 7 StartRoot 49 - x2 EndRoot dx
1. What substitution will be the most helpful for evaluating this​integral?
2. Find dx?
3. Rewrite the given integral using substitution.

Answer 1

Explanation:

1. Given the integral function
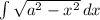`\int\limits {\sqrt{a^(2) -x^(2) } } \, dx`, using trigonometric substitution, the substitution that will be most helpful in this case is substituting x as
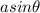`asin \theta` i.e
`x = a sin\theta`.

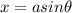All integrals in the form
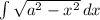`\int\limits {\sqrt{a^(2) -x^(2) } } \, dx` are always evaluated using the substitute given where 'a' is any constant.

From the given integral,
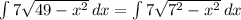`\int\limits {7\sqrt{49-x^(2) } } \, dx = \int\limits {7\sqrt{7^(2) -x^(2) } } \, dx` where a = 7 in this case.

The substitute will therefore be
`x = 7 sin\theta`

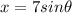
2.) Given
`x = 7 sin\theta`

`(dx)/(d \theta) = 7cos \theta`

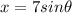
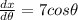
cross multiplying

`dx = 7cos\theta d\theta`

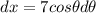
3.) Rewriting the given integral using the substiution will result into;

`\int\limits {7\sqrt{49-x^(2) } } \, dx \\= \int\limits {7\sqrt{7^(2) -x^(2) } } \, dx\\= \int\limits {7\sqrt{7^(2) -(7sin\theta)^(2) } } \, dx\\= \int\limits {7\sqrt{7^(2) -49sin^(2)\theta } } \, dx\\= \int\limits {7\sqrt{49(1-sin^(2)\theta)} } } \, dx\\= \int\limits {7\sqrt{49(cos^(2)\theta)} } } \, dx\\since\ dx = 7cos\theta d\theta\\= \int\limits {7\sqrt{49(cos^(2)\theta)} } } \, 7cos\theta d\theta\\= \int\limits {7\{7(cos\theta)} }}} \, 7cos\theta d\theta\\`

`= \int\limits343 cos^(2) \theta \, d\theta`