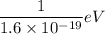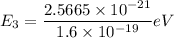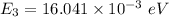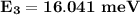Answer:
the energy of the third excited rotational state
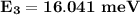
Step-by-step explanation:
Given that :
hydrogen chloride (HCl) molecule has an intermolecular separation of 127 pm
Assume the atomic isotopes that make up the molecule are hydrogen-1 (protium) and chlorine-35.
Thus; the reduced mass μ =
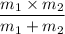
μ =

μ =
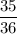
∵ 1 μ = 1.66 × 10⁻²⁷ kg
μ =
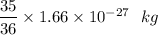
μ = 1.6139 × 10⁻²⁷ kg
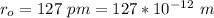
The rotational level Energy can be expressed by the equation:
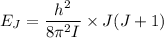
where ;
J = 3 ( i.e third excited state) &
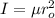
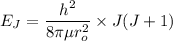
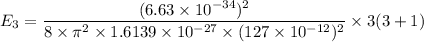
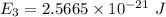
We know that :
1 J =