Answer:
The expected value of the points earned on a single roll in this game is
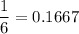 .
.
Explanation:
We are given that consider a game in which players roll a number cube to determine the number of points earned. If a player rolls a prime number, that many points will be added to the player’s total. Any other roll will be deducted from the player’s total.
Assuming that the numbered cube is a dice with numbers (1, 2, 3, 4, 5, and 6).
Here, the prime numbers are = 1, 2, 3 and 5
Numbers which are not prime = 4 and 6
This means that if the dice got the number 1, 2, 3 or 5, then that many points will be added to the player’s total and if the dice got the number 4 or 6, then that many points will get deducted from the player’s total.
Here, we have to make a probability distribution to find the expected value of the points earned on a single roll in this game.
Note that the probability of getting any of the specific number on the dice is
 .
.
Numbers on the dice (X) P(X)
+1
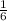
+2
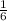
+3
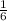
-4
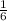
+5
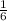
-6
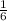
Here (+) sign represent the addition in the player's total and (-) sign represents the deduction in the player's total.
Now, the expected value of X, E(X) =
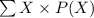
=
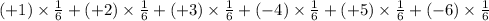
=

=
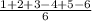
=
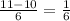
Hence, the expected value of the points earned on a single roll in this game is
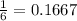 .
.