Question

Of the boxes of cruncho cereal on a supermarket shelf 25 percent contain a prize and the other 75 percent contain no prize.if Gerry buys two boxes of cruncho cereal which of the following is closest to the probability that neither box contain a prize?


`(7)/(10)`

`(9)/(16)`

`(3)/(4)`

`(15)/(16)`


​

Answer 1

`X \sim Binom(n=2, p=0.25)`

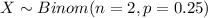
And for this case we want to find the following probability:

`P(X=0)`

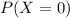
And we can use the probability mass function given by:

`P(X) = nCx (p)^x *1-p)^(n-x)`

And replacing we got:

`P(X=0)= (2C0) (0.25)^0 (1-0.25)^(2-0)= 0.5625= (9)/(16)`

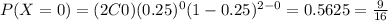
Explanation:

For this problem we can define the random variable of interest X as "the number of bxes with a cereal" and for this problem we can model the variable with the following distribution:

`X \sim Binom(n=2, p=0.25)`

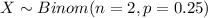
And for this case we want to find the following probability:

`P(X=0)`

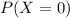
And we can use the probability mass function given by:

`P(X) = nCx (p)^x *1-p)^(n-x)`

And replacing we got:

`P(X=0)= (2C0) (0.25)^0 (1-0.25)^(2-0)= 0.5625= (9)/(16)`