Question

Un depósito de gran superficie se llena de agua hasta una altura de 0,3 m. En el fondo del depósito hay un orificio de 5 cm2 de sección por el que sale el agua con un chorro continuo. A) ¿Qué cantidad de líquido saldrá del depósito expresada en m3/s?

Answer 1

a) El caudal de salida del chorro es
`1.213* 10^(-3)\,(m^(3))/(s)`.

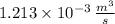Step-by-step explanation:

a) Asúmase que el tanque se encuentra a presión atmósferica y que la sima del tanque tiene una altura de 0 metros. La rapidez de salida del chorro del depósito se determined a partir del Principio de Bernoulli, cuya línea de corriente entre la cima y la sima del tanque queda descrita por la siguiente ecuación:

`\Delta z = (v_(out)^(2))/(2\cdot g)`

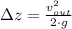
Donde:

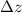`\Delta z` - Diferencia de altura, medida en metros.

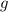`g` - Constante gravitacional, medida en metros por segundo al cuadrado.

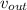`v_(out)` - Rapidez de salida del chorro, medida en metros por segundo.

Se despeja la rapidez de salida del chorro:

`v_(out) = √(2\cdot g \cdot \Delta z)`

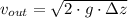
Si
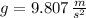`g = 9.807\,(m)/(s^(2))` y
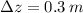`\Delta z = 0.3\,m`, entonces la rapidez de salida del chorro es:

`v_(out) = \sqrt{2\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (0.3\,m)}`

`v_(out) \approx 2.426\,(m)/(s)`

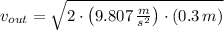
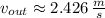
Ahora, la cantidad de líquido que sale del depósito por unidad de tiempo se obtiene al multiplicar la rapidez de salida del chorro por el área transversal del orificio. Esto es:

`\dot V_(out) = v_(out)\cdot A_(t)`

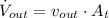
Donde:

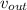`v_(out)` - Rapidez de salida del chorro, medida en metros por segundo.

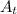`A_(t)` - Área transversal del orificio, medido en metros cuadrados.

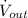`\dot V_(out)` - Caudal de salida del chorro, medido en metros cúbicos por segundo.

Dado que
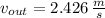`v_(out) = 2.426\,(m)/(s)` y
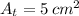`A_(t) = 5\,cm^(2)`, el caudal de salida del chorro es:

`\dot V_(out) = \left(2.426\,(m)/(s) \right)\cdot (5\,cm^(2))\cdot \left((1)/(10000)\,(m^(2))/(cm^(2)) \right)`

`\dot V_(out) = 1.213* 10^(-3)\,(m^(3))/(s)`

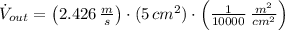
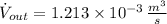
El caudal de salida del chorro es
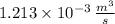`1.213* 10^(-3)\,(m^(3))/(s)`.