Question

Does anyone know the answer to the table below?

Answer 1

Hey there! :)

Answer:

16 minutes.

Explanation:

Create an equation in the form y = mx + b to solve this problem. Begin by solving for the rate of change of the table using the slope formula:

`m = \frac{\text{rise}}{\text{run}} = (y_2 - y_1)/(x_2 - x_1)`

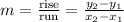
Plug in values from the table into the equation:

`m = (64 - 40)/(9 - 5)`

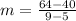
Simplify:

`m = (24)/(4)`

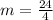
m = 6.

Plug in the slope and a point from the table into the equation

y = mx + b

40 = 6(5) + b

40 = 30 + b

40 - 30 = b

b = 10.

Rewrite the equation:

y = 6x + 10

To solve for how long it took her to ride 1 km, plug 1 into the equation:

y = 6(1) + 10

y = 6 + 10

y = 16 minutes.